参考
微分和导数的区别
导数的古典定义
微分为一个函数在自变量做无穷小变化时函数值的变化。给定x的变化dx,则对应到f(x)的变化为df,df就等于f导数乘dx。
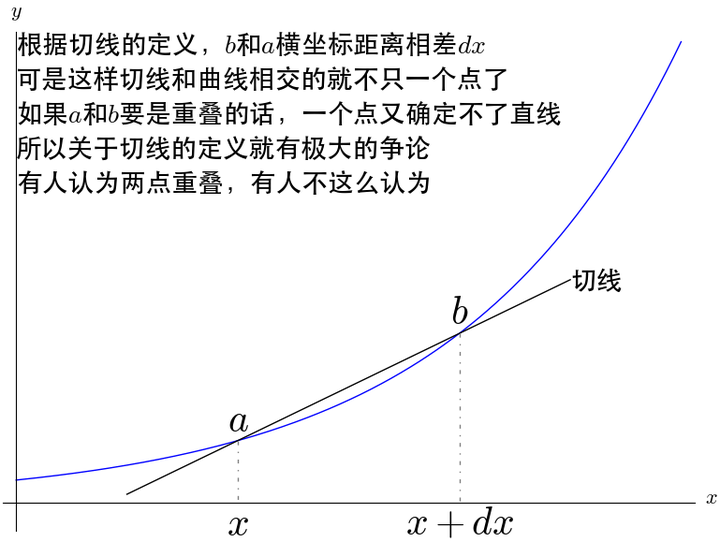
这里因为dx的定义问题,产生了麻烦,导致微积分的基础不牢固。

又譬如如上对dx的处理。在第五步处理中,dx被视作非0处理。在第六步处理中,却又被视作0处理。
- 古典微积分总结
- 切线:通过无穷小量定义了切线
- 导数:导数就是切线的斜率
- 微分:微分就是微小的增量,即无穷小量
基于极限重建微积分
即完全摒弃无穷小量,基于极限的概念,重新建立微积分
- 1 极限
- 使用 epsilon & delta 来描述极限:
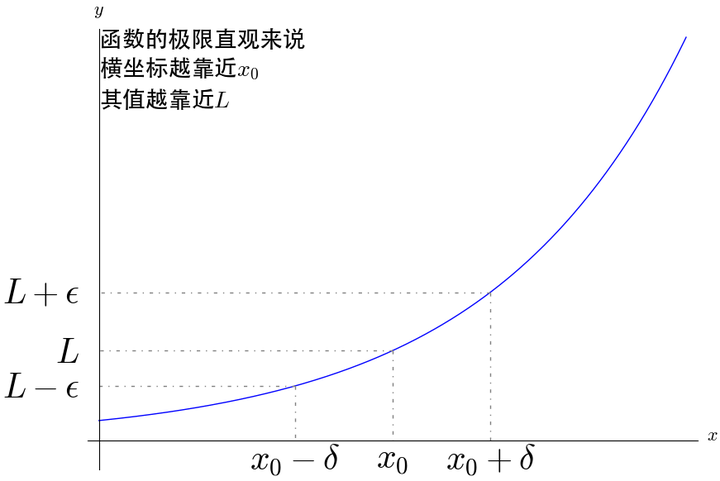
- 极限的定义:无无穷小量的存在
- 使用 epsilon & delta 来描述极限:
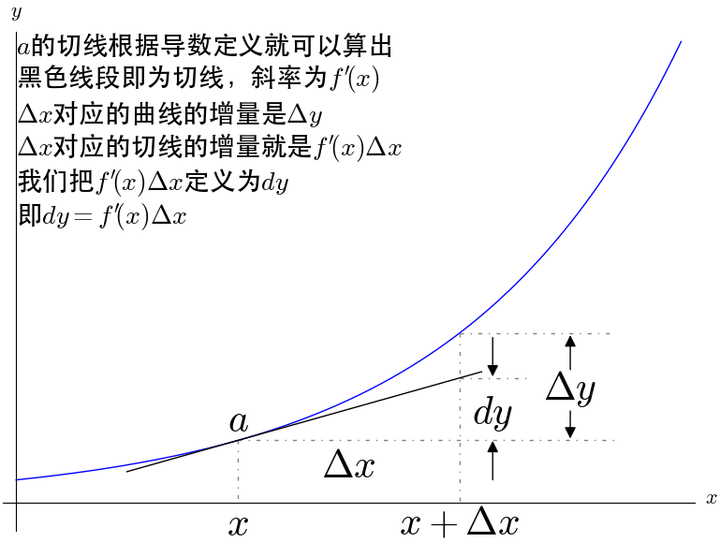
- 2 导数的极限定义

- 极限定义的导数,脱离了微商的概念,此时导数更应该被看作为一个整体。
- 通过导数,我们仍可以定义什么是微分。原先是先定义了微分再有导数,现在是先定义了导数再有的微分。
- 3.对于极限微积分的总结
- 导数:被定义为一个极限,其意义就是变化率
- 微分:是一个线性函数,其意义就是变化的具体数值
- 切线:有了导数之后就可以被确定下来
古典微积分和极限微积分的对比
- 古典微积分先定义微分,再定义导数,极限微积分先定义导数再定义微分。
- 古典微积分的导数基于无穷小量定义,极限微积分的导数是基于极限定义的。
- 意义在于,无穷小量此时是一个实体。可以比较,可以运算。
- 例如:无穷小量之间的比较,实际为实体关于无穷小量收敛速度的比较。
- 意义在于,无穷小量此时是一个实体。可以比较,可以运算。
- 古典微积分的微分是无穷小量,极限微积分的微分是一个线性函数。
- 古典微积分的定积分是求无穷小矩形面积的和,极限微积分的定积分是求黎曼和。
- 古典微积分的切线是可以画出来的,极限微积分的切线是算出来的。
- 古典微积分的建立过程很直观,极限微积分的建立过程更抽象。
总结
- 导数为函数在某点上的变化率,是一个数。
- 为函数在某点上的切线的斜率
- 微分为函数在某点上的线性表达,是一个函数。
- 看似近似,是因为微分本身使用了导数来定义。